Μέχρι και σήμερα ακονίζει το μυαλό δυνατών λυτών. Η αναδιάταξη απλών γεωμετρικών σχημάτων σε νέους σύνθετους σχηματισμούς αποτελεί το πιο οικείο «μαθηματικό» παιχνίδι. Η μαγεία του παιχνιδιού άγγιξε τη μαθηματική σκέψη του Αρχιμήδη.
Όπως φαίνεται σε έργο του, που το μοναδικό αντίγραφο σώθηκε μερικώς από το Παλίμψηστο, ο Αρχιμήδης προσπάθησε να εντοπίσει γεωμετρικές σχέσεις στο αρχαιότερο γνωστό παζλ. Το «(ο)στομάχιον» ήταν πνευματικό παιχνίδι της αρχαιότητας. Το παιχνίδι απαρτίζεται από ένα τετράγωνο που έχει διαιρεθεί σε 14 γεωμετρικά σχήματα. Σκοπός του παιχνιδιού είναι ο παίχτης να διαμορφώσει ξανά το τετράγωνο με όσους περισσότερους τρόπους μπορεί, χρησιμοποιώντας όλα τα κομμάτια του.
Η αρχική κατασκευή της επιφάνειας έγινε με τη χρήση ξύλου. Όταν διαιρέθηκε το ξύλο στα 14 κομμάτια, οι γραμμές που δημιουργήθηκαν πάνω σε αυτό ήταν εμφανείς. Έτσι ο παίχτης μπορούσε χωρίς ιδιαίτερη δυσκολία να ενώσει τις γραμμές και να σχηματίσει το τετράγωνο ξανά.

Το επίπεδο δυσκολίας ανέβηκε όταν χρησιμοποιήθηκε ελεφαντόδοντο για την κατασκευή του παιχνιδιού. Πάνω σε αυτό το υλικό οι γραμμές που χαράζονταν για να κοπεί η επιφάνεια δεν ήταν εμφανείς. Γι’ αυτό και μία πιθανή ερμηνεία για το οστομάχιον προέρχεται από τη μάχη των οστών του ελέφαντα.
Το οστομάχιον αποτελούσε πρόγονο και του τάνγκραμ καθώς μία άλλη χρήση του παιχνιδιού ήταν να διαμορφωθούν με τα 14 κομμάτια κάποιες συγκεκριμένες φιγούρες. Τα τελικά σχήματα αποτελούσαν ζώα, όπως μία χήνα που πετάει, έναν ελέφαντα, ένα αγριογούρουνο, ένα σκυλί, που γαβγίζει. Υπήρχαν και φιγούρες που προέρχονταν από μορφές και κατασκευές της καθημερινότητας, όπως μία κολόνα, ένας πύργος, ένας κυνηγός ή ένας πολεμιστής.
Παράλληλα το οστομάχιον αποτελούσε ένα μαθηματικό πρόβλημα του Αρχιμήδη για τους μαθητές του. Ο Αρχιμήδης απέδειξε ότι ο λόγος του εμβαδού ενός τεμαχίου προς το εμβαδόν του τετραγώνου είναι ρητός αριθμός.
Το μαθηματικό πρόβλημα του Αρχιμήδη
Το 1906 ο Δανός καθηγητής Johan Ludvig Heiberg σε επίσκεψη του στην Κωνσταντινούπολη, εξέτασε μία περγαμηνή, γραμμένη το 13ο αιώνα μ.Χ., η οποία περιείχε 174 σελίδες λειτουργικών κειμένων. Η περγαμηνή τελικά ήταν παλίμψηστο, δηλαδή ένα έγγραφο που με κείμενο, που είχε γραφτεί πάνω από σβησμένη εργασία.
Σήμερα εικάζεται από τη μελέτη του παλίμψηστου ότι ο Αρχιμήδης πιθανόν προσπάθησε να υπολογίσει τον συνολικό αριθμό των διαφορετικών συνδυασμών που σχηματίζουν τετράγωνο.

Το απαιτητικό ερώτημα συνδυαστικής απαντήθηκε το 2003 από τον Bill Culter με την χρήση υπολογιστών. Υπάρχουν 536 διαφορετικοί συνδυασμοί για να σχηματίσει κανείς το τετράγωνο. Αν συμπεριλάβει κανείς τις συμμετρίες με περιστροφές, κατοπτρισμούς και πανομοιότυπα τρίγωνα, οι συνδυασμοί υπολογίζονται στους 17152.
mixanitouxronou
Οστομάχιον by wikipedia
Οστομάχιον ονομαζόταν ένα μαθηματικό κείμενο του Αρχιμήδη. Μόνο λίγα αποσπάσματα σε αραβικά και βυζαντινά χειρόγραφα έχουν διασωθεί. Ενώ τα αραβικά χειρόγραφα αποδίδουν λάθος τον τίτλο, (Στομάχιον), ο Ρωμαίος συγγραφέας Ausonius ορθώς το ονομάζει «Ostomachion» («quod Graeci ostomachion vocavere»), όπως αποκαλύπτει ο Johann L. Heiberg, ο Δανός μελετητής του Αρχιμήδη.
Η λέξη οστομάχιον προέρχεται από τις λέξεις οστούν και μάχη και σημαίνει η μάχη των οστών.
Ήταν διαδεδομένο παιχνίδι στην αρχαιότητα και έμοιαζε με το σημερινό τάνγκραμ. Παιζόταν με 14 γεωμετρικά σχήματα (οστά) με τα οποία δύο ή και περισσότεροι παίχτες κάναν διάφορες γεωμετρικές φιγούρες και ανταγωνίζονταν μεταξύ τους.
Δεν είναι γνωστό, αν ένα από τα δυο (το παιχνίδι ή το μαθηματικό πρόβλημα) είναι αρχαιότερο του άλλου.
Περιγραφή του παιχνιδιού
Παίζεται με 14 γεωμετρικά σχήματα που στο σύνολο τους σχηματίζουν ένα τετράγωνο.
Ο Ausonius και άλλοι αρχαίοι συγγραφείς αναφέρουν τις εξής φιγούρες:
μια περικεφαλαία
μια χήνα που πετάει
έναν πύργο
μια κολόνα
έναν ελέφαντα
ένα αγριογούρουνο
ένα σκυλί που γαβγίζει
έναν κυνηγό που παραμονεύει
έναν αρματωμένο πολεμιστή.

Το μαθηματικό πρόβλημα
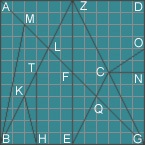
Το μαθηματικό πρόβλημα αναφέρεται στο αραβικό κείμενο που μετέφρασε ο Heinrich Suter στα γερμανικά (Archimedis opera omnia, vol. 2, S. 420 ff., ed. J. L. Heiberg, Leipzig 1881):
«Σχεδιάζουμε ένα ορθογώνιο παραλληλόγραμμο με γωνίες ΑΒΓΔ,
τέμνουμε την πλευρά ΒΓ στο σημείο κέντρου Ε,
σχεδιάζουμε το τμήμα ΕΖ κάθετα στο ΒΓ,
τραβούμε την διαγώνιο ΑΓ, ΒΖ και ΖΓ,
τέμνουμε το ΒΕ στο σημείο κέντρου Η,
και τραβούμε την κάθετο ΗΤ κάθετα στην ΒΕ.
Κατόπιν, βάζουμε τον χάρακα στο σημείο Η
και με στόχο το Α σχηματίζουμε την γραμμή ΗΚ,
τέμνουμε την ΑΛ στην μέση στο σημείο Μ
και τραβούμε την γραμμή ΒΜ.
Το αρχικό τετράγωνο ΑΒΓΔ χωρίστηκε σε επτά γεωμετρικές επιφάνειες.
Σημειώνουμε το κεντρικό σημείο Ν του τμήματος ΓΔ,
το κεντρικό σημείο Σ του ΖΓ,
τραβούμε το ΕΣ,
τοποθετούμε τον χάρακα στα σημεία Β και Σ
και τραβούμε τις γραμμές ΣΟ και ΣΝ
Έτσι χωρίσαμε το τετράγωνο Ζ-Γ σε επτά γεωμετρικές επιφάνειες,
και ολόκληρο το τετράγωνο σε 14 γεωμετρικές επιφάνειες.
Θα αποδείξουμε, ότι για κάθε ένα από τα 14 κομμάτια ισχύει, ότι το εμβαδόν του τετραγώνου είναι ακέραιο πολλαπλάσιο του εμβαδού του τμήματος.